构建你自己的代码解释器 - 使用 o3-mini 的动态工具生成和执行

2025年2月3日
在 Github 中打开

为 LLM 代理提供与外部世界或其他代理交互能力的核心是“工具（或函数）调用”，其中 LLM 可以使用参数调用函数（代码块）。通常，这些函数由开发人员预先定义，并附带其预期的输入和输出。然而，在本 Cookbook 中，我们探索了一种更灵活的范例 - 使用 LLM 模型（在本例中为 **o3-mini**）**动态生成工具**，并使用代码解释器执行工具。

使用代码解释器的动态生成工具调用

动态生成工具是由 LLM 自身在运行时根据用户提示创建的函数或代码块。这意味着您不必在代码库中预定义每种可能的场景——从而实现更开放、更具创造性和适应性的问题解决。

动态生成工具调用更进一步，赋予 LLM 生成工具和即时执行代码块的能力。这种动态方法对于以下任务尤其有用：

  • 数据分析和可视化
  • 数据 manipulation 和转换
  • 机器学习工作流程生成和执行
  • 流程自动化和脚本编写
  • 以及更多，随着通过实验出现新的可能性

使用 o3-mini 进行动态工具生成

o3-mini 模型于 2025 年 1 月 31 日发布，具有出色的 STEM 能力——在科学、数学和编码方面尤为突出——同时保持了小型模型的低成本和低延迟。在本 Cookbook 中，我们将演示 o3-mini 生成 Python 代码以解释数据和提取见解的能力。

推理模型特别擅长生成动态工具来分析数据，因为它们可以自行推理，而无需显式的思维链提示。事实上，提供显式的思维链指令可能会干扰模型的内部推理，并导致次优结果。您可以在这里了解更多关于 o3-mini 的信息。

为什么构建你自己的代码解释器

许多 API 提供商——例如 OpenAI 的 Assistants API——提供内置的代码解释器功能。这些内置的代码解释器可能非常强大，但在某些情况下，开发人员可能需要创建自己的自定义代码解释器。例如

  1. **语言或库支持**：内置解释器可能不支持您的任务所需的特定编程语言（例如，C++、Java 等）或库。
  2. **任务兼容性**：您的用例可能与提供商的内置解决方案不兼容。
  3. **模型限制**：您可能需要提供商的解释器不支持的语言模型。
  4. **成本考虑**：代码执行或模型使用的成本结构可能不符合您的预算或限制。
  5. **文件大小**：输入数据的文件大小太大或提供商的解释器不支持。
  6. **与内部系统集成**：提供商的解释器可能无法与您的内部系统集成。

您将学到什么

通过遵循本 Cookbook，您将学习如何：

  • 使用 Docker 设置隔离的 Python 代码执行环境
  • 为 LLM 代理配置您自己的代码解释器工具
  • 建立清晰的“代理”关注点分离，以确保安全
  • 使用 **o3-mini** 模型动态生成用于数据分析的代码
  • 编排代理以高效完成给定的任务
  • 设计一个可以动态生成和执行代码的代理应用程序

您将学习如何从头开始构建自定义代码解释器工具，利用 LLM 的强大功能生成复杂的代码，并在隔离的环境中安全地执行该代码——所有这些都是为了使您的 AI 驱动的应用程序更灵活、更强大且更具成本效益。

示例场景

我们将使用 Key Factors Traffic Accidents 提供的示例数据来回答一系列问题。这些问题不需要预先定义，我们将赋予 LLM 生成代码来回答此类问题的能力。

示例问题可能包括：

  • 哪些因素对事故频率的贡献最大？（特征重要性分析）
  • 哪些区域发生事故的风险最高？（分类/聚类）
  • 交通罚款金额如何影响事故数量？（回归/因果推断）
  • 我们能否确定减少事故率的最佳罚款金额？（优化模型）
  • 更高的罚款是否与更低的平均速度或减少的事故相关？（相关性/回归）
  • 等等...

使用传统的**预定义工具调用**方法，开发人员需要为每个问题预先定义函数。这限制了 LLM 回答未在预定义函数集中定义的任何其他问题的能力。我们通过使用**动态工具调用**方法克服了这一限制，其中 LLM 生成代码并使用代码解释器工具执行代码。

概述

让我们深入了解构建这个具有动态生成工具调用的代理应用程序的步骤。此应用程序包含三个组件：

步骤 1：设置隔离的代码执行容器环境

我们需要一个安全的环境来执行 LLM 生成的函数调用。我们希望避免直接在主机上运行 LLM 生成的代码，因此将创建一个资源访问受限的 Docker 容器环境（例如，没有网络访问）。默认情况下，Docker 容器无法访问主机的文件系统，这有助于确保 LLM 生成的任何代码都受到限制。

⚠️ 注意事项：为 LLM 生成的代码实施强大的防护措施

LLM 可能会生成具有意外后果的有害代码。作为最佳实践，隔离代码执行环境，仅提供任务所需的资源访问权限。避免在您的主机或笔记本电脑上运行 LLM 生成的代码。

步骤 2：定义和测试代理

“什么是代理？” 在本 Cookbook 的上下文中，代理是：

  1. LLM 要遵循的一组指令，即开发人员提示
  2. 一个 LLM 模型，以及通过 API 调用模型的能力
  3. 工具调用访问函数，以及执行函数的能力

我们将定义两个代理：

  1. FileAccessAgent：此代理将读取文件并将上下文提供给 PythonCodeExecAgent。
  2. PythonCodeExecAgent：此代理将生成 Python 代码以回答用户的问题，并在 Docker 容器中执行代码。

步骤 3：设置代理编排以运行应用程序

根据应用程序需求，有多种编排代理的方法。在本示例中，我们将使用简单的编排，其中用户提供任务，然后按顺序调用代理以完成任务。

整体编排如下所示：

让我们开始吧

先决条件

在开始之前，请确保您的主机上已安装并配置了以下内容：

  1. Docker：已安装并在您的本地计算机上运行。您可以在这里安装它。
  2. Python：已安装在您的本地计算机上。您可以在这里安装它。
  3. OpenAI API 密钥：在您的本地计算机上设置为环境变量或根目录下的 .env 文件。您可以在这里设置它。

步骤 1：设置隔离的代码执行环境

让我们定义一个 Docker 化的容器环境，用于执行我们的代码。我已经在 resources/docker 目录下定义了 dockerfile，它将用于创建具有以下规范的容器环境：

  • Python 3.10 作为基础
  • 非 root 用户
  • 预安装 requirements.txt 中的包

docker 镜像创建过程中包含的 requirements.txt 包含 LLM 生成的代码可能需要完成其任务的所有潜在包。鉴于我们将限制容器的网络访问，因此我们需要预先安装任务所需的包。出于安全目的，我们的 LLM 将不允许安装任何其他包。

您可以使用语言要求（例如 Python 3.10）创建自己的 docker 镜像，并预先安装任务所需的包，或者使用特定语言（例如 Java、C++ 等）和任务所需的包创建自定义 docker 镜像。

让我们使用以下命令构建 docker 镜像。为了简洁起见，我已将输出重定向以 grep 成功消息，并在构建失败时打印消息。

!docker build -t python_sandbox:latest ./resources/docker 2>&1 | grep -E "View build details|ERROR" || echo "Build failed."
View build details: docker-desktop://dashboard/build/desktop-linux/desktop-linux/kl8fo02q7rgbindi9b42pn1zr

让我们在受限模式下运行容器。容器将在后台运行。这是我们定义容器安全策略的机会。最佳实践是仅允许容器执行任务所需的最低限度功能。默认情况下，容器无法从容器内部访问主机文件系统。让我们也限制其网络访问，使其无法访问 Internet 或任何其他网络资源。

# Run the container in restricted mode. The container will run in the background.
!docker run -d --name sandbox --network none --cap-drop all --pids-limit 64 --tmpfs /tmp:rw,size=64M   python_sandbox:latest sleep infinity
8446d1e9a7972f2e00a5d1799451c1979d34a2962aa6b4c35a9868af8d321b0e

让我们使用 docker ps 确保容器正在运行，它应该列出我们的容器。

!docker ps 
CONTAINER ID   IMAGE                   COMMAND            CREATED         STATUS         PORTS     NAMES
8446d1e9a797   python_sandbox:latest   "sleep infinity"   2 seconds ago   Up 2 seconds             sandbox

步骤 2：定义和测试代理

为了我们的目的，我们将定义两个代理。

  1. 代理 1：文件访问代理（使用预定义工具调用）
  • 指令：理解文件内容，以作为 Agent 2 的上下文。
  • 可以访问主机的文件系统。
  • 可以从主机读取文件并将其复制到 Docker 容器中。
  • 无法访问代码解释器工具。
  • 使用 gpt-4o 模型。
  1. 代理 2：Python 代码生成器和执行器（使用动态生成工具调用和代码执行）
  • 从 Agent 1 接收文件内容的上下文。
  • 指令：生成 Python 脚本以回答用户的问题。
  • 可以访问 Docker 容器内的代码解释器，该解释器用于执行 Python 代码。
  • 仅可访问 Docker 容器内的文件系统（而非主机）。
  • 无法访问主机的文件系统或网络。
  • 使用我们最新的 **o3-mini** 模型，该模型擅长代码生成。

文件访问（Agent 1）与代码生成器和执行器（Agent 2）的这种关注点分离对于防止 LLM 直接访问或修改主机至关重要。

限制 Agent 1 使用静态工具调用，因为它有权访问主机文件系统。

代理工具调用类型访问主机文件系统访问 Docker 容器文件系统访问代码解释器
代理 1：文件访问预定义工具是是否
代理 2：Python 代码生成器和执行器动态生成工具否是是

为了保持代理和工具的组织性，我们定义了一组核心类，这些类将用于创建两个代理以保持一致性，并使用面向对象编程原则。

  • **BaseAgent**：我们从一个抽象基类开始，该基类强制执行通用方法签名，例如 task()。基类还提供用于调试的记录器、语言模型接口和其他通用函数，例如 add_context()，用于向代理添加上下文。
  • **ChatMessages**：一个用于存储对话历史记录的类，因为 ChatCompletions API 是无状态的。
  • **ToolManager**：一个用于管理代理可以调用的工具的类。
  • **ToolInterface**：任何代理可以调用的“工具”的抽象类，以便工具具有一致的接口。

这些类在 object_oriented_agents/core_classes 目录中定义。

定义代理 1：带有 FileAccessTool 的 FileAccessAgent

让我们从定义继承自 ToolInterface 类的 FileAccessTool 开始。**FileAccessTool** 工具在 resources/registry/tools 目录的 file_access_tool.py 文件中定义。

  • FileAccessTool 实现了 ToolInterface 类，这确保了工具将具有一致的接口。
  • 在 get_definition 方法中绑定 OpenAI Function Calling API 的工具定义，以及工具的 run 方法，确保了可维护性、可扩展性和可重用性。

现在，让我们定义扩展 BaseAgent 类的 **FileAccessAgent**，并将 **FileAccessTool** 绑定到代理。FileAccessAgent 在 resources/registry/agents 目录的 file_acess_agent.py 文件中定义。FileAccessAgent 是：

  • BaseAgent 类的具体实现。
  • 使用开发人员提示、模型名称、记录器和语言模型接口进行初始化。如果需要，开发人员可以覆盖这些值。
  • 具有一个 setup_tools 方法，该方法将 FileAccessTool 注册到工具管理器。
  • 具有一个 task 方法，该方法调用 FileAccessTool 读取文件并将上下文提供给 PythonCodeExecAgent。
  • model_name='gpt-4o'，它为任务提供了足够的推理和工具调用能力。

定义代理 2：带有 PythonExecTool 的 PythonExecAgent

类似地，PythonExecTool 继承自 ToolInterface 类，并实现了 get_definition 和 run 方法。get_definition 方法返回 OpenAI Function Calling API 期望的工具定义格式。run 方法在 Docker 容器中执行 Python 代码并返回输出。此工具在 resources/registry/tools 目录的 python_code_interpreter_tool.py 文件中定义。

同样，PythonExecAgent 是 BaseAgent 类的具体实现。它在 resources/registry/agents 目录的 python_code_exec_agent.py 文件中定义。PythonExecAgent 是：

  • BaseAgent 类的具体实现。
  • 使用开发人员提示、模型名称、记录器和语言模型接口进行初始化。如果需要，开发人员可以覆盖这些值。
  • 具有一个 setup_tools 方法，该方法将 PythonExecTool 注册到工具管理器。
  • 具有一个 task 方法，该方法调用 OpenAI API 来执行用户的任务，在本例中，该任务涉及生成 Python 脚本以回答用户的问题，并使用代码解释器工具运行它。
  • model_name='o3-mini'，它擅长 STEM 任务，例如代码生成。
  • reasoning_effort='high'，考虑到任务的复杂性，它允许更完整的推理，但代价是生成更多 token 和更慢的响应。默认值为 medium，这是速度和推理准确性之间的平衡。

您可以在这里了解更多关于 reasoning_effort 参数的信息。

步骤 3：设置代理编排以运行应用程序

定义了代理之后，现在我们可以定义编排循环来运行应用程序。此循环将提示用户提出问题或任务，然后调用 FileAccessAgent 读取文件并将上下文提供给 PythonExecAgent。PythonExecAgent 将生成 Python 代码以回答用户的问题，并在 Docker 容器中执行代码。代码执行的输出将显示给用户。

用户可以输入“exit”停止应用程序。我们的问题：**哪些因素对事故频率的贡献最大？** 请注意，我们没有预先定义回答此问题的函数。

# Import the agents from registry/agents

from resources.registry.agents.file_access_agent import FileAccessAgent
from resources.registry.agents.python_code_exec_agent import PythonExecAgent


prompt = """Use the file traffic_accidents.csv for your analysis. The column names are:
Variable	Description
accidents	Number of recorded accidents, as a positive integer.
traffic_fine_amount	Traffic fine amount, expressed in thousands of USD.
traffic_density	Traffic density index, scale from 0 (low) to 10 (high).
traffic_lights	Proportion of traffic lights in the area (0 to 1).
pavement_quality	Pavement quality, scale from 0 (very poor) to 5 (excellent).
urban_area	Urban area (1) or rural area (0), as an integer.
average_speed	Average speed of vehicles in km/h.
rain_intensity	Rain intensity, scale from 0 (no rain) to 3 (heavy rain).
vehicle_count	Estimated number of vehicles, in thousands, as an integer.
time_of_day	Time of day in 24-hour format (0 to 24).
accidents	traffic_fine_amount
"""


print("Setup: ")
print(prompt)

print("Setting up the agents... ")

# Instantiate the agents with the default constructor defined values
# Developer may override the default values - prompt, model, logger, and language model interface if needed

# This agent use gpt-4o by default
file_ingestion_agent = FileAccessAgent()

# Let's make sure agent uses o3-mini model and set the reasoning_effort to high
data_analysis_agent = PythonExecAgent(model_name='o3-mini', reasoning_effort='high')

print("Understanding the contents of the file...")
# Give a task to the file ingestion agent to read the file and provide the context to the data analysis agent 
file_ingestion_agent_output = file_ingestion_agent.task(prompt)

# Add the file content as context to the data analysis agent
# The context is added to the agent's tool manager so that the tool manager can use the context to generate the code 

data_analysis_agent.add_context(prompt)
data_analysis_agent.add_context(file_ingestion_agent_output)

while True:

    print("Type your question related to the data in the file. Type 'exit' to exit.")
    user_input = input("Type your question.")

    if user_input == "exit":
        print("Exiting the application.")
        break

    print(f"User question: {user_input}")

    print("Generating dynamic tools and using code interpreter...")
    data_analysis_agent_output = data_analysis_agent.task(user_input)

    print("Output...")
    print(data_analysis_agent_output)

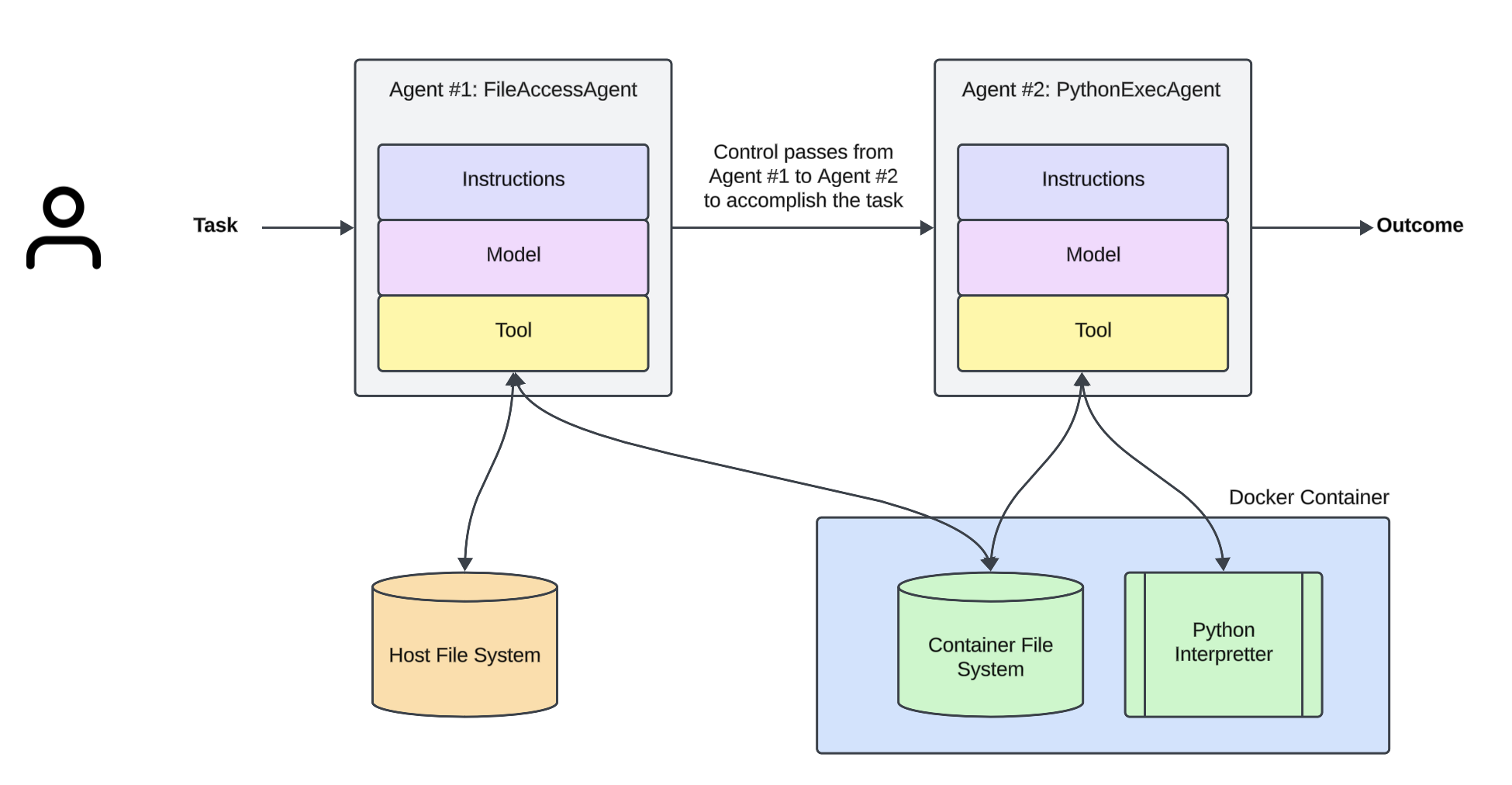
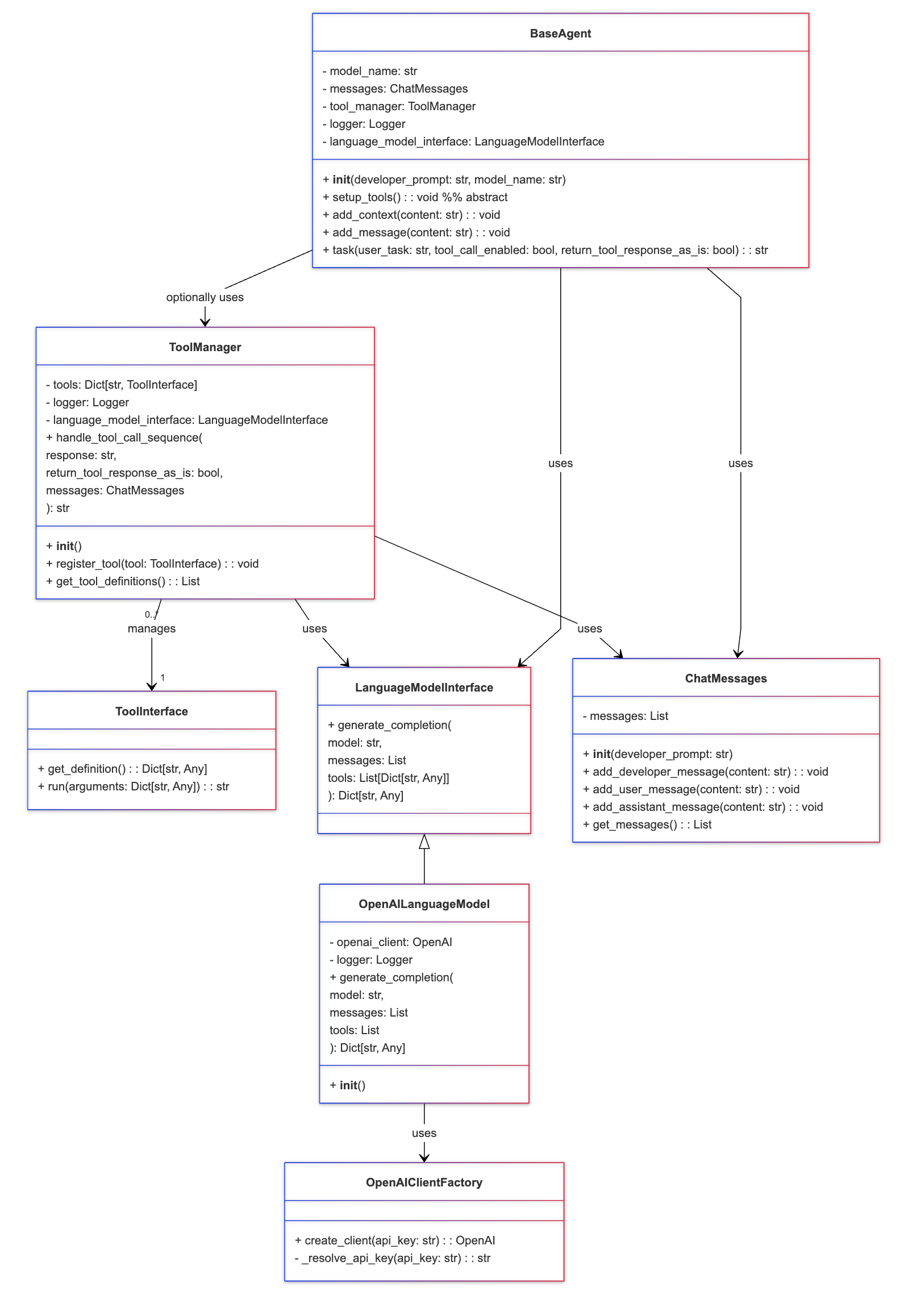
Setup: 
Use the file traffic_accidents.csv for your analysis. The column names are:
Variable	Description
accidents	Number of recorded accidents, as a positive integer.
traffic_fine_amount	Traffic fine amount, expressed in thousands of USD.
traffic_density	Traffic density index, scale from 0 (low) to 10 (high).
traffic_lights	Proportion of traffic lights in the area (0 to 1).
pavement_quality	Pavement quality, scale from 0 (very poor) to 5 (excellent).
urban_area	Urban area (1) or rural area (0), as an integer.
average_speed	Average speed of vehicles in km/h.
rain_intensity	Rain intensity, scale from 0 (no rain) to 3 (heavy rain).
vehicle_count	Estimated number of vehicles, in thousands, as an integer.
time_of_day	Time of day in 24-hour format (0 to 24).
accidents	traffic_fine_amount

Setting up the agents... 
Understanding the contents of the file...

2025-02-03 13:03:54,066 - MyApp - INFO - Handling tool call: safe_file_access
2025-02-03 13:03:54,067 - MyApp - INFO - Tool arguments: {'filename': './resources/data/traffic_accidents.csv'}
2025-02-03 13:03:54,562 - MyApp - INFO - Tool 'safe_file_access' response: Copied ./resources/data/traffic_accidents.csv into sandbox:/home/sandboxuser/.
The file content for the first 15 rows is:
    accidents  traffic_fine_amount  traffic_density  traffic_lights  pavement_quality  urban_area  average_speed  rain_intensity  vehicle_count  time_of_day
0          20               4.3709           2.3049         753.000            0.7700           1        321.592          1.1944       290.8570     160.4320
1          11               9.5564           3.2757           5.452            4.0540           1        478.623          6.2960       931.8120       8.9108
2          19               7.5879           2.0989           6.697          345.0000           0        364.476          2.8584       830.0860       5.5727
3          23               6.3879           4.9188           9.412            4.7290           0         20.920          2.1065       813.1590     131.4520
4          23               2.4042           1.9610           7.393            1.7111           1         37.378          1.7028         1.4663       6.9610
5          31               2.4040           6.7137           5.411            5.9050           1        404.621          1.8936       689.0410       8.1801
6          29               1.5228           5.2316           9.326            2.3785           1         16.292          2.5213       237.9710      12.6622
7          18               8.7956           8.9864           4.784            1.9984           0        352.566          1.9072       968.0670       8.0602
8          15               6.4100           1.6439           5.612            3.6090           1        217.198          3.4380       535.4440       8.2904
9          22               7.3727           8.0411           5.961            4.7650           1        409.261          2.0919       569.0560     203.5910
10         28               1.1853           7.9196           0.410            3.7678           1        147.689          1.6946       362.9180     224.1580
11         17               9.7292           1.2718           8.385            8.9720           0         46.888          2.8990       541.3630     198.5740
12         14               8.4920           3.9856           1.852            4.6776           0        287.393          2.2012        75.2240       2.3728
13         21               2.9111           1.7015           5.548            1.9607           1        176.652          1.0320       566.3010       6.9538
14         22               2.6364           2.5472           7.222            2.3709           0        209.686          4.0620        64.4850     170.7110

Type your question related to the data in the file. Type 'exit' to exit.
User question: What factors contribute the most to accident frequency?
Generating dynamic tools and using code interpreter...

2025-02-03 13:04:39,427 - MyApp - INFO - Handling tool call: execute_python_code
2025-02-03 13:04:39,429 - MyApp - INFO - Tool arguments: {'python_code': "import pandas as pd\nimport numpy as np\nfrom sklearn.linear_model import LinearRegression\nfrom sklearn.preprocessing import StandardScaler\nimport matplotlib.pyplot as plt\nimport seaborn as sns\n\n# Load the dataset\nfile_path = '/home/sandboxuser/traffic_accidents.csv'\ndf = pd.read_csv(file_path)\n\n# Show basic information\nprint('Dataset shape:', df.shape)\nprint('First few rows:')\nprint(df.head(), '\\n')\nprint('Columns:', df.columns.tolist(), '\\n')\n\n# Correlation matrix analysis\ncorr_matrix = df.corr()\nprint('Correlation matrix:')\nprint(corr_matrix, '\\n')\n\n# Correlation of each feature with accidents\nacc_corr = corr_matrix['accidents'].drop('accidents').sort_values(key=lambda x: abs(x), ascending=False)\nprint('Correlation of other variables with accidents (sorted by absolute correlation):')\nprint(acc_corr, '\\n')\n\n# Visualize the correlation matrix\nplt.figure(figsize=(10, 8))\nsns.heatmap(corr_matrix, annot=True, cmap='coolwarm', fmt='.2f')\nplt.title('Correlation Matrix')\nplt.tight_layout()\nplt.savefig('correlation_matrix.png')\nplt.close()\n\n# Prepare data for regression analysis\n# Exclude target variable 'accidents'\nfeatures = [col for col in df.columns if col != 'accidents']\nX = df[features]\ny = df['accidents']\n\n# Standardize the features to compare the regression coefficients on the same scale\nscaler = StandardScaler()\nX_scaled = scaler.fit_transform(X)\n\n# Fit a linear regression model\nmodel = LinearRegression()\nmodel.fit(X_scaled, y)\n\n# Gather coefficients along with feature names\ncoef = model.coef_\ncoef_df = pd.DataFrame({'Feature': features, 'Coefficient': coef})\ncoef_df['AbsCoefficient'] = coef_df['Coefficient'].abs()\ncoef_df = coef_df.sort_values(by='AbsCoefficient', ascending=False)\nprint('Linear Regression Coefficients (using standardized features):')\nprint(coef_df[['Feature', 'Coefficient']], '\\n')\n\n# Additionally, compute feature importances using a Random Forest regressor\nfrom sklearn.ensemble import RandomForestRegressor\nrf = RandomForestRegressor(random_state=42)\nrf.fit(X, y)\nrf_importance = rf.feature_importances_\nrf_df = pd.DataFrame({'Feature': features, 'Importance': rf_importance})\nrf_df = rf_df.sort_values(by='Importance', ascending=False)\nprint('Random Forest Feature Importances:')\nprint(rf_df, '\\n')\n\n# The printed outputs will help in understanding which factors contribute most to accident frequency.\n\n# For clarity, save the coefficients and importances to CSV files (optional)\ncoef_df.to_csv('linear_regression_coefficients.csv', index=False)\nrf_df.to_csv('random_forest_importances.csv', index=False)\n\n# End of analysis\n"}
2025-02-03 13:04:43,123 - MyApp - INFO - Tool 'execute_python_code' response: Dataset shape: (8756, 10)
First few rows:
   accidents  traffic_fine_amount  ...  vehicle_count  time_of_day
0         20               4.3709  ...       290.8570     160.4320
1         11               9.5564  ...       931.8120       8.9108
2         19               7.5879  ...       830.0860       5.5727
3         23               6.3879  ...       813.1590     131.4520
4         23               2.4042  ...         1.4663       6.9610

[5 rows x 10 columns] 

Columns: ['accidents', 'traffic_fine_amount', 'traffic_density', 'traffic_lights', 'pavement_quality', 'urban_area', 'average_speed', 'rain_intensity', 'vehicle_count', 'time_of_day'] 

Correlation matrix:
                     accidents  traffic_fine_amount  ...  vehicle_count  time_of_day
accidents             1.000000            -0.745161  ...       0.068399     0.101995
traffic_fine_amount  -0.745161             1.000000  ...      -0.016610    -0.006236
traffic_density      -0.059265            -0.004365  ...      -0.014244     0.002806
traffic_lights       -0.026642             0.009056  ...       0.001373    -0.001971
pavement_quality      0.064694            -0.021229  ...       0.007840     0.000055
urban_area            0.145092            -0.005136  ...      -0.006053    -0.006320
average_speed         0.093923             0.009151  ...       0.000777    -0.005338
rain_intensity       -0.091673            -0.015302  ...      -0.025933    -0.013446
vehicle_count         0.068399            -0.016610  ...       1.000000    -0.009303
time_of_day           0.101995            -0.006236  ...      -0.009303     1.000000

[10 rows x 10 columns] 

Correlation of other variables with accidents (sorted by absolute correlation):
traffic_fine_amount   -0.745161
urban_area             0.145092
time_of_day            0.101995
average_speed          0.093923
rain_intensity        -0.091673
vehicle_count          0.068399
pavement_quality       0.064694
traffic_density       -0.059265
traffic_lights        -0.026642
Name: accidents, dtype: float64 

Linear Regression Coefficients (using standardized features):
               Feature  Coefficient
0  traffic_fine_amount    -3.891935
4           urban_area     0.739618
5        average_speed     0.533698
6       rain_intensity    -0.532251
8          time_of_day     0.512661
1      traffic_density    -0.331997
7        vehicle_count     0.281283
3     pavement_quality     0.264987
2       traffic_lights    -0.092800 

Random Forest Feature Importances:
               Feature  Importance
0  traffic_fine_amount    0.580838
1      traffic_density    0.165201
6       rain_intensity    0.095124
8          time_of_day    0.035814
5        average_speed    0.035590
3     pavement_quality    0.032177
2       traffic_lights    0.022613
7        vehicle_count    0.021006
4           urban_area    0.011637 



Output...
The analysis shows that one variable stands out by far:

• Both the simple correlation analysis and regression results indicate that traffic_fine_amount is the dominant factor—its correlation with accidents is strong (about –0.75), and in the standardized linear regression its coefficient is the largest in magnitude (around –3.89). The negative sign suggests that, in this data, higher fine amounts are associated with fewer accidents (which might reflect more stringent enforcement or deterrence).

Other findings include:

• The Random Forest model also ranks traffic_fine_amount as most important (importance ≈ 0.58), with the next most influential factor being traffic_density (importance ≈ 0.17). Although its simple correlation with accidents is lower, traffic_density may contribute non‐linearly.

• Additional factors like urban_area, average_speed, rain_intensity, and time_of_day have moderate associations (with linear model coefficients ranging between about ±0.5 to +0.74). These suggest that accidents tend to be somewhat higher in urban areas and vary with time of day and weather conditions, but their overall impact is much less than that of traffic fine amounts.

In summary, the data analysis indicates that traffic_fine_amount contributes the most to accident frequency—with higher fines linked to fewer recorded accidents—while factors such as traffic density, urban area status, vehicle speed, rain intensity, and time of day also play secondary roles.
Type your question related to the data in the file. Type 'exit' to exit.
Exiting the application.

在本示例中，**o3-mini** 根据用户的问题动态生成了一个工具（Python 脚本）来分析数据。请注意，**o3-mini** 使用了多种方法来检查问题，例如相关性分析、线性回归和随机森林模型。这种方法突出了以下几点：

**reasoning_effort**：模型执行推理的深度，例如，在本例中方法的数量，通常在参数从 low、medium 增加到 high 时增加。您可以尝试不同的推理 effort 水平以查看差异。

**动态生成工具调用**：用于分析数据的工具（Python 脚本）不是由开发人员手动编写或预先确定的。相反，o3-mini 模型在运行时创建了相关的数据探索和相关性分析代码。

**隔离的代码执行**：为了确保安全并避免在主机上运行不受信任的代码，Python 脚本是在 Docker 容器中使用 execute_python_code 工具执行的。此容器具有受限的资源访问权限（例如，没有网络和有限的文件系统访问权限），从而最大限度地减少了任意代码执行带来的潜在风险。

结论

本 Cookbook 为开发定制的代码解释器提供了指南，该解释器根据特定的应用程序需求量身定制，解决了供应商提供的解决方案中发现的限制，例如语言约束、成本考虑以及使用不同 LLM 或模型的灵活性需求。

**管理代理和工具的方法**：我们还定义了一组核心类来管理代理和工具。这种方法确保了代理和工具将具有一致的接口，并且可以在不同的应用程序中重用。可以创建一个代理和工具的存储库，例如 registry 文件夹，以管理代理和工具。

**o3-mini 模型**：我们演示了 o3-mini 模型在运行时生成复杂代码的能力，以根据用户最少的提示分析数据。然后 o3-mini 模型对分析结果进行推理，向用户解释结果。

最后，**总结一下**，构建具有动态工具调用的代理应用程序的三个步骤是：

  1. 设置隔离的代码执行容器环境
  2. 定义和测试代理
  3. 设置代理编排以运行应用程序

我们讨论了隔离代码执行环境以确保安全并避免在主机上运行不受信任的代码的重要性。通过 CSV 文件的用例，我们演示了如何动态生成工具（Python 脚本）来分析数据并回答用户的问题。我们还展示了如何在 Docker 容器中执行代码并将输出返回给用户。